원문 논문: A decision-making model for blasting risk assessment in mines using FBWM and GRA methods
🔗 DOI: https://www.nature.com/articles/s41598-024-82181-5 * 해당 논문은 무료로 볼 수 있다.
1. 이 논문을 읽게 된 이유
산업안전에 종사하는 분이나, 산업안전 관련하여 자격증을 취득한 분이라면 위험성 평가방법들 중 HAZOP, JSA, FMEA를 들어본 적이 있을것이다. 이러한 전통적인 위험성 평가방법은 작업장의 특성위험 요소를 분석하고, 그 위험성이 얼마나 높은지 평가하기 위해 위험 우선순위 번호(RPN)을 계산하여 예방 조치를 수립하는 방법이다. 하지만 이러한 평가방법에는 여러가지 단점이 있는데,
- 기준 가중치 할당 없음: 기존 방법들은 위험 평가 기준{C(결과), P(발생 가능성), E(노출) 등}에 대한 가중치를 부여하지 않기 때문에 작업 유형에 따라 중요한 기준이 간과될 수 있다.
- 동일한 위험 우선순위 번호(RPN) 부여 가능성: 사전 결정된 데이터와 테이블을 기반으로 위험을 계산 및 우선순위화하기 때문에 두 개의 서로 다른 위험이 동일한 RPN을 가질 수 있다.
- 불확실성 존재: 전문가들의 경험과 지식 수준이 다르기 때문에 평가 과정에서 불확실성이 발생할 수 있다.
이러한 단점을 해결하기 위해 여러가지 논문들이 나오고 있는데, 그 중에서 기존 위험성 평가기법에 FBWM과 GRA기법을 혼합한 논문을 소개하고자 한다.
2. 논문요약
논문에서는 기존 위험 평가 방법의 민감도와 정확도를 높이고자 FBWM(퍼지 최선-최악 방법)과 GRA(회색 관계 분석) 기법을 결합한 새로운 위험 평가 모델을 제안했다. 본 논문의 주요 기여점은 다음과 같다.
1. 퍼지 집합 이론 적용: 인간의 판단 과정에서 발생하는 모호성을 해결하기 위해 퍼지집합을 활용하여 의사결정을 개선함
2. FBWM 기법을 활용한 기준 가중치 할당: 기존의 Fine–Kinney 방법의 한계를 극복하여 위험 평가의 정확성을 높임.
3. GRA 기법을 활용한 위험 우선순위화: 위험 요소를 효과적으로 순위화하여 합리적인 의사결정을 지원.
4. 언어적 변수 활용: Crisp(단일 수치) 값 대신 언어적 변수를 사용하여 평가의 불확실성을 줄임.
기존 위험 평가 방법으로 Fine–Kinney 기법을 사용하였는데, 위험도(Risk Score, R)는 다음 공식으로 계산된다.

공식 변수 설명
- R(Risk Score, 위험 점수) = 최종적으로 계산된 위험 수준
- C(Consequence, 결과) = 사고가 발생했을 때의 영향 또는 심각도
- P(Probability, 발생 확률) = 사고가 발생할 가능성
- E(Exposure, 노출 빈도) = 위험에 노출되는 빈도

우선 FBWM과 GRA 기법을 알아보기 전에, 퍼지 집합 이론에 대해 알아야 한다. 전통적인 집합 이론에서는 어떤 요소가 완전히 포함(1)되거나, 완전히 제외(0)되는 방식으로 정의된다.
하지만 현실에서는 경계가 불분명한 개념이 많기 때문에 퍼지 집합에서는 연속적인 소속 값을 사용하여 좀 더 유연한 방법으로 데이터를 표현할 수 있다. 논문에서는 삼각 퍼지 수(TFN)를 사용하여 데이터를 표현했다.
삼각 퍼지 수(TFN)란 세 개의 값 (L, M, U)로 정의되며, 각각 최솟값(L), 중심값(M), 최댓값(U)을 의미한다.
예를 들어, 시험 점수(0~100점)를 평가한다고 가정하면, "좋은 점수(Good Score)"를 퍼지 숫자로 표현할 때, 아래와 같이 표현할 수 있다.
- L = 60 (최소한 이 점수 이상은 되어야 함)
- M = 80 (이 점수가 가장 대표적인 좋은 점수임)
- U = 100 (이 점수 이하까지는 좋은 점수로 인정됨)
퍼지 집합에서는 어떤 값이 특정 집합에 속하는 정도를 나타내기 위해 소속 함수(µ, Membership Function)를 사용한다.
논문에서 사용한 소속 함수 공식은 다음과 같다.


퍼지 수를 단일 값(정확한 수치)로 변환하는 방법으로 논문에서는 다음과 같은 공식을 사용했다.

퍼지집합을 이제 알았으니, FBWM(Fuzzy Best-Worst Method)을 알아보겠다.
FBWM는 기준(크리테리아, Criteria)들의 중요도를 결정하는 방법인데, 여러 가지 평가 기준 중 가장 중요한 것(Best)과 가장 덜 중요한 것(Worst)을 선정하고, 이를 비교하여 각 기준의 가중치(Weight)를 계산하는 방법이다. 기존 BWM(Best-Worst Method)의 한계를 보완한 퍼지(Fuzzy) 버전으로, 인간의 모호한 판단을 더 정확하게 반영할 수 있다.
FBWM은 다음 6단계로 진행되는데,
① 평가 기준(크리테리아) 설정:
평가해야 할 기준을 정한다. 논문에서는 폭파 위험을 평가하기 위해 Fine–Kinney 기준을 사용했다.
- C (Consequence, 결과)
- P (Probability, 발생 확률)
- E (Exposure, 노출)
② 가장 중요한(Best)과 가장 덜 중요한(Worst) 기준 선택:
전문가들이 가장 중요한 기준(C_best)과 가장 덜 중요한 기준(C_worst)을 선택하는데, 논문에서는 "C (결과)"가 가장 중요하고, "E (노출)"가 가장 덜 중요한 것으로 선정하였다.
③ Best-to-Others (B2O) 비교:
가장 중요한 기준(Best)과 나머지 기준들을 비교한다.

예를 들어, "C"가 "P"보다 보통 중요하다면,

논문에서 사용된 언어적 변수와 퍼지 숫자 변환표는 아래와 같다.

④ Others-to-Worst (O2W) 비교:
각 기준들이 가장 덜 중요한 기준(Worst)과 비교된다.
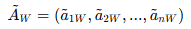
예를 들어, "P"가 "E"보다 약간 더 중요하다면,
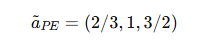
⑤ 퍼지 가중치(Fuzzy Weights) 계산:
이제 퍼지 선형 최적화(Fuzzy Linear Optimization)를 사용하여 각 기준의 가중치를 계산한다.
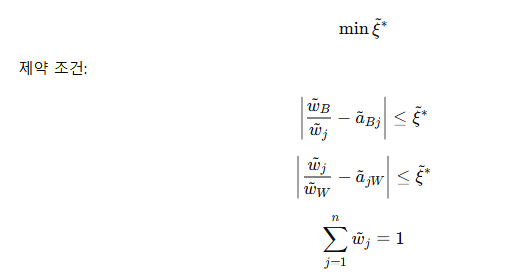
⑥ 퍼지 가중치를 단일 숫자(Defuzzification)로 변환:
퍼지 가중치를 단일 값으로 변환할 때, 논문에서는 다음 공식을 사용했다.
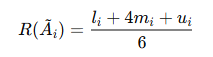
이제 FBWM에 대한 개념을 학습했으니, 이를 활용하여, 광산 발파 위험 평가의 우선순위를 매겨보자.
먼저, 전문가 4명이 아래와 같이 파악한 폭파 작업의 위험요소들(20가지)*에 대해 언어적 평가(linguistic terms)를 한다.
* 여기에서는 10가지만 사용해서 설명함
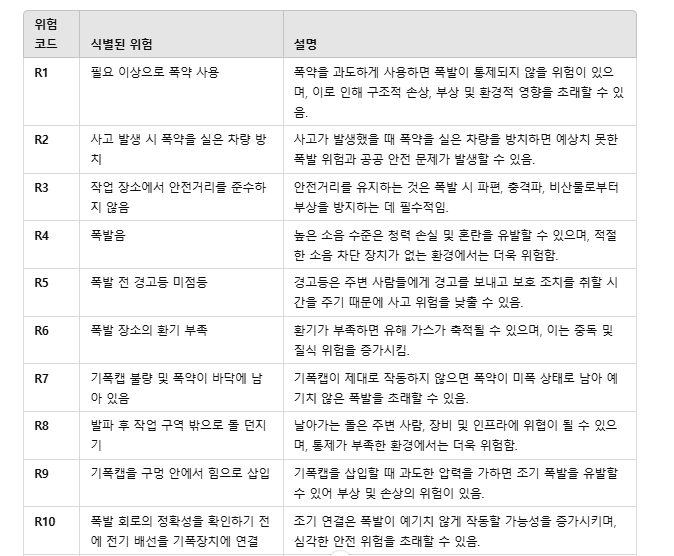
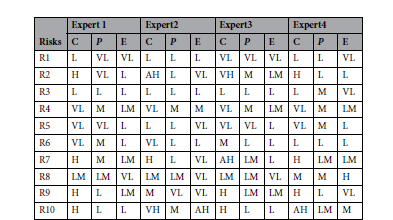
그 다음 전문가들의 언어적 평가를 퍼지 숫자(TFN)로 변환한다. 논문에서는 변환할 때, 아래의 변환표를 이용하였다.
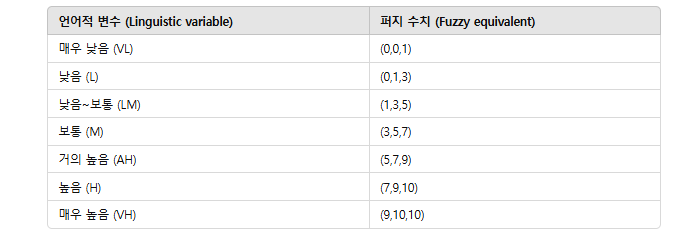
각 위험요소에 대해 4명의 전문가가 평가한 퍼지 숫자를 평균낸다.
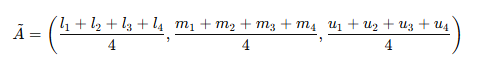
즉, 전문가 4명의 하한(l) 값 평균, 전문가 4명의 중간(m) 값 평균, 전문가 4명의 상한(u) 값 평균을 각각 구하여 최종 퍼지 숫자를 만들고, 퍼지 숫자를 단일 값으로 변환하면 아래와 같은 표를 얻을 수 있다.
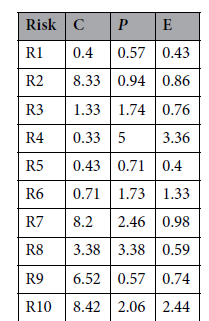
이제 위에서 배운 FBWM을 활용하여 C, P, E에 대한 퍼지 가중치를 계산한다. 위에서 얘기한 것 처럼 논문에서는 "C (결과)"가 가장 중요하고, "E (노출)"가 가장 덜 중요한 것으로 선정했다.

① 퍼지 가중치를 아래와 같이 설정하고,
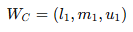
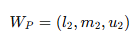
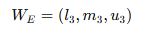
② Best 기준과 다른 기준을 비교
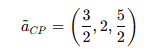
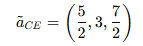
③ 다른기준과 Worst 기준을 비교
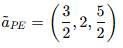
④ 퍼지 선형 최적화(Fuzzy Linear Optimization)를 사용하여 제약 조건을 만족하는 범위 내에서 최적의 가중치를 계산(심 플렉스 알고리즘(Simplex Algorithm) 등을 이용)하고, 단일값 변환식에 대입한다.
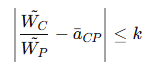
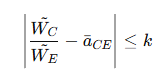
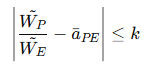
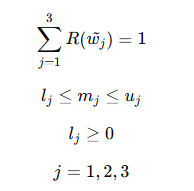
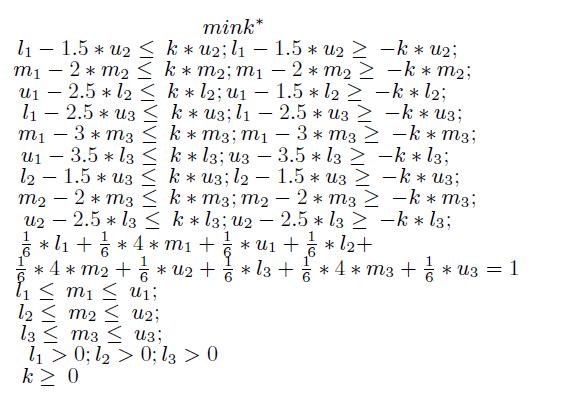
그러면 아래와 같은 가중치와 단일값을 구할 수 있다.
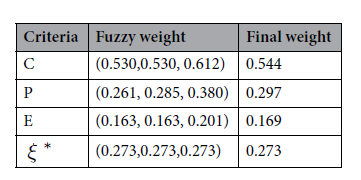
이제 GRA를 구하기 위해 각 위험요소에 대한 퍼지 숫자를 단일 값으로 변환한 표에서 최대-최소 정규화(Min-Max Normalization)를 적용하여 값을 변환하면 아래와 같은 표를 얻을 수 있다.

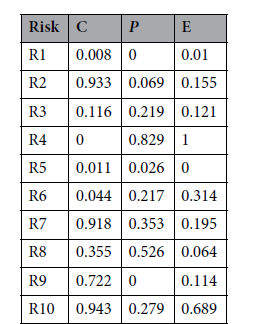
정규환된 표에서 아래의 GRA공식을 사용하면

아래와 같은 각 위험요인에 대한 GRA값이 구해진다.
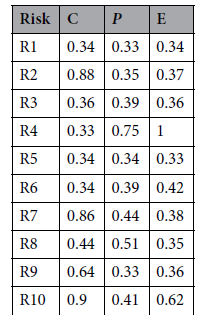
마지막으로 민감도 분석(Sensitivity Analysis)을 수행하기 위해 가중치(W1)를 적용하여 위 표에 가중치를 곱하면
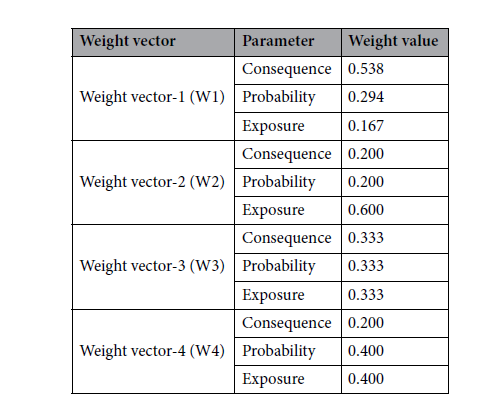
아래와 같이 가중치 벡터(W1)과 곱한 GRA 값의 계산되고 각 위험요인에 대한 GRA값을 합산하면 우선순위가 구해진다.
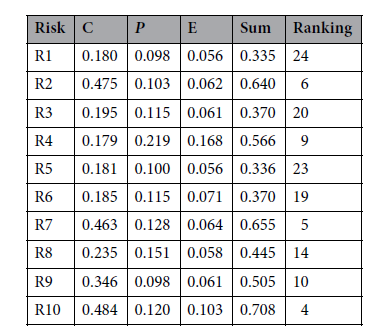
아래 표는 민감도 분석을 위한 가중치 벡터(W1, W2, W3, W4)를 이용해서 구한 우선순위 표랑 그래프이다.
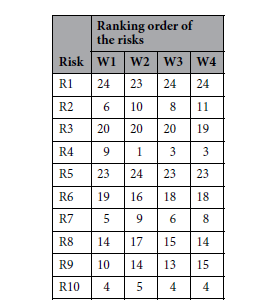
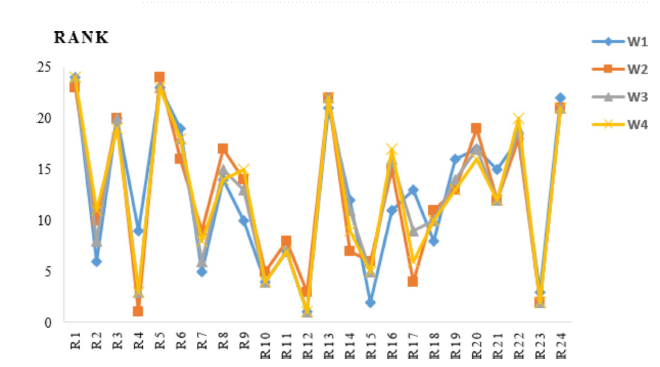
위 표에 따르면, 가중치 조합을 변경하면 위험 순위도 달라진다. 예를 들어, 결과(C)의 가중치를 높이면 심각한 위험이 우선적으로 평가되며, 발생 확률(P) 또는 노출 빈도(E)를 강조하면 다른 위험 요소들이 더 중요하게 고려된다. 하지만, 주요 위험 요소의 순위는 기존 방법과 대체로 일치하여 민감도가 작다.
두 번째 단계에서는 기존 다기준 의사결정 기법(MCDM)과 비교하여 제안된 모델의 위험 우선순위 결과를 평가했다.
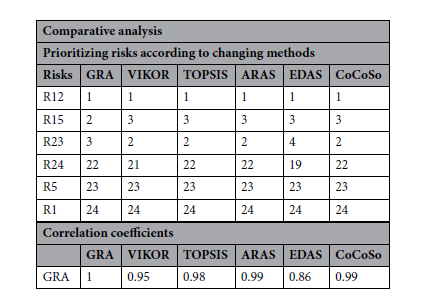
이 또한, 주요 위험 요소의 순위는 기존 방법과 대체로 일치했으며, 일부 순위 차이는 각 기법의 분석 방식 차이 때문으로 이러한 차이는 의사결정 과정에 큰 영향을 미치지 않는다. 따라서, 제안된 모델이 기존 기법과 높은 일관성을 갖는다는 것을 검증했다.
3. 개인적 해석
이 논문은 가중치 설정을 조정함으로써 위험 요소의 우선순위가 달라질 수 있음을 실증적으로 보여준다.
이는 특정 산업이나 상황에 맞춰 위험 평가 방식을 유연하게 조정할 수 있다는 점에서 실무적으로 매우 유용하다.
예를 들어, 건설업에서는 노출 빈도(E)를, 금융업에서는 발생 확률(P)를 더 중요한 요소로 설정하여 맞춤형 위험 평가를 수행할 수 있다. 그러나 의사결정자가 임의로 가중치를 설정할 경우, 분석 결과가 주관적으로 변할 가능성이 높다는 점이 한계로 작용할 수 있다.
따라서, 논문에서 가중치 설정에 대한 명확한 가이드라인을 제시하지 않은 점이 아쉬운 부분이다.
만약 이러한 가이드라인이 마련된다면, 안전 관리 소프트웨어나 프로젝트 리스크 관리 시스템에 이 모델을 적용하여 실시간으로 위험 순위를 조정하고, 의사결정자에게 최적의 대응 방안을 자동으로 추천하는 기능을 개발할 수 있을 것이다.
이를 통해 리스크 관리의 효율성을 높이고, 보다 정밀한 의사결정을 지원할 수 있을 것으로 기대된다.
'논문 리뷰' 카테고리의 다른 글
| 안전 관리 시스템: 문헌의 광범위한 개요 (0) | 2025.02.06 |
|---|---|
| 위험과 예측 불가능한 요소를 이해, 평가 및 관리하는 새로운 관점 (0) | 2025.02.06 |
| 협력 로봇 시스템을 위한 ISO 15066 표준 검토 (0) | 2025.02.04 |
| 주요 위험 산업에서 안전 표준 사용이 안전에 미치는 영향 평가 (0) | 2025.01.31 |